Apostar em esportes é algo imprevisível, por isso o apostador analisa o jogo e o estuda para tomar uma decisão que julga ser mais provável. Uma forma de melhor ajudá-lo na tomada de decisões é através da distribuição de Poisson.
Algumas pessoas acham Poisson complicado, difícil de entender, o que é verdade, mas o apostador sério não vai fechar seus olhos para algo que o beneficie.
A meu ver vale muito a pena fazer um esforço para entender algo que expressa a probabilidade de uma série de eventos ocorrer num determinado período.
Poisson em apostas esportivas vai calcular probabilidades percentuais para cada resultado que procura, assim você poderá ver a probabilidade do mandante de vencer a partida, de dar visitante ou de dar empate, além de cálculos para Unders (menos) e Overs (mais) gols.
Então, como você pode ver, Poisson é necessário para você saber a frequência do evento ocorrer, e a partir daí você poderá encontrar apostas de valor.
Poisson em apostas esportivas
Neste artigo explicarei tudo e com calma, o máximo detalhado que puder, supondo que você não saiba absolutamente nada. Irei exemplificar as coisas usando algo que nos interessa, ou seja, futebol.
Primeiro, a equação de Poisson: Essa equação é confusa, mas acalme-se. Primeiro de tudo, utilizei Barcelona como exemplo na equação de Poisson porque eles sempre marcam muitos gols.
Agora, vamos supor que eles estão jogando em casa contra o Villarreal e queremos saber a probabilidade de cada resultado ocorrer. Para isso, a primeira coisa a se fazer é determinar a probabilidade de o Barcelona marcar x gols.
Isso significa que aqueles pequenos x (um símbolo) que aparece 2 vezes na equação ao lado do µ e do ! pode ser substituído por números. Então digamos que estou interessado em calcular a probabilidade do Barça marcar 2 gols, assim a equação se torna:
P (Barcelona marcará 2 Gols) = µ2 x e -µ / 2!
Aposto que agora as coisas se tornaram um pouco mais claras para você. Sabe aquele símbolo estranho, o µ? Isso é um espaço reservado para a “expectativa de gols” do Barcelona. E como saber isso?
Há sites como o understated e o infogol que divulgam alguns desses dados de forma gratuita. Esses dados são conhecidos como expected goals.
Vou ligar o símbolo µ ao número aleatório de 2.59, que é o xG (expected goals) do Barça neste meu exemplo hipotético. Falarei mais sobre isso abaixo.
Isso significa que nossa equação será:
P (Barcelona marcará 2 Gols) = 2.59² x e -2.59 / 2!
A equação está tomando uma cara, e podemos facilmente dividir o que temos em três partes: as duas primeiras são multiplicadas e depois divididas pela inferior. Os três pequenos componentes individualmente são:
- – 2.592
- – e -2.59
- – 2!
Agora vou falar de cada um deles. No primeiro (1) item, o pequeno número 2 acima de 2,59 significa “elevado ao quadrado”. Então, para este caso, se multiplica 2,59 por 2,59.
- – 2.592 = (2.59 X 2.59) = 6.7081
- – e -2.59
- – 2!
(Mas e se o número de gols esperado for 3 ou 4 e não 2? Basta uma calculadora científica para lhe ajudar. Você pode encontrar isso pesquisando por calculadora no Google ou abrindo a calculadora científica do Windows. Então multiplique o valor do símbolo µ, usado aqui por nós como expectativa de gols, pelo x, que no exemplo queremos saber sobre 2 gols do Barça. Se quiséssemos multiplicar por 3 e não por 2, você deveria digitar o valor do símbolo µ, apertar Xy e então calcular)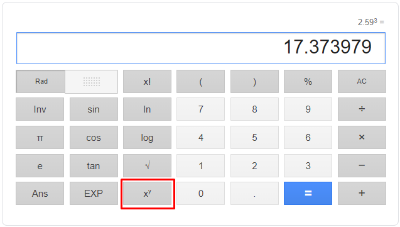
Voltando ao nosso cálculo e recapitulando, x é a probabilidade de o Barcelona marcar 2 gols e µ é a expectativa de gols marcados e isso irei falar depois.
Falta o símbolo e e ele é uma constante matemática que pode ser trocado pelo valor 2.718281828459 (ou 2.71). Assim temos uma pequena equação, em que 2.718281828459 é elevado ao potencial µ (-2.59). Então a conta 2.718281828459 x potencial de -2.59 = 0.07502, ou simplesmente:
Na calculadora digite 2.718281828459. Multiplica esse valor por x^y (igual na imagem acima), digite -2.59 e calcule.
- – 2.592 = (2.59 X 2.59) = 6.7081
- – e -2.59 = (2.718281828459 x potencial de -2.59) = 0.07502
- – 2!
Nós estamos quase chegando lá.
Agora sobrou o item 3, e essa é a mini-equação “2!”. Isso significa 2 fatorial. Isso pode parecer difícil, mas não é tanto.
Fatorial de 0: 0! (lê-se 0 fatorial)
0! = 1
Fatorial de 1: 1! (lê-se 1 fatorial)
1! = 1
Fatorial de 2: 2! (lê-se 2 fatorial)
2! = 2 . 1 = 2
Fatorial de 3: 3! (lê-se 3 fatorial)
3! = 3 . 2 . 1 = 6
Fatorial de 4: 4! (lê-se 4 fatorial)
4! = 4. 3 . 2 . 1 = 24
…e assim por diante. Não é difícil. Então nosso fatorial é o terceiro exemplo que eu dei aqui, nos dando a resposta de 2.
- – 2.592 = (2.59 X 2.59) = 6.7081
- – e -2.59 = (2.718281828459 x potencial de -2.59) = 0.07502
- – 2! = (2 X 1) = 2
Agora vamos voltar à equação, substituindo todos os símbolos pelos números que foram calculados.
(não necessariamente coloque 2.718281828459 na calculadora, coloque 2.71 que está bom)
P (Barcelona marcará 2 Gols) = 6.7081 x 0.07502 / 2!

Então, a probabilidade (P) de o Barcelona marcar 2 gols é 0.2516. A conta (6.7081 X 0.07502) / 2 = 0.2516.
Acima, tudo o que eu fiz foi explicar como calcular Poisson em apostas esportivas para encontrar a probabilidade de o Barcelona fazer 2 gols.
Espero que você tenha aprendido, porque usando este sistema é possível calcular a probabilidade de o Barcelona marcar qualquer quantidade de gols. Abaixo uma tabela da qualidade de gols usando este mesmo método:
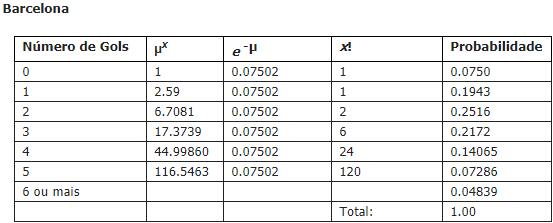
Se ficou confuso para você, volte o texto e procure ler com calma para entender cada ponto. Apenas vá com calma e atenção para as coisas terem sentido.
Tudo que foi abordado acima, inclusive na tabela, é a probabilidade de o Barcelona marcar gols. Mas estamos falando de apostas esportivas, então também precisamos fazer o mesmo com o Villarreal.
O cálculo a ser feito é exatamente igual, teremos que encontrar a expectativa de gols do Villarreal (µ). Vamos dizer que é de 0.52.
Não acho necessário refazer toda explicação, então já vou colocar o resultado em uma tabela para adiantar.
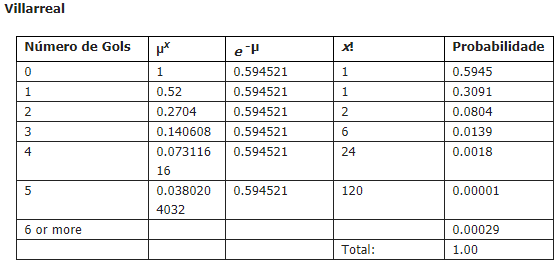
Agora as coisas ficaram interessantes porque podemos a partir dessas duas tabelas calcular qualquer resultado que estamos pensando.
Qual a chance do Barcelona ganhar de 2-0?
Isso é fácil de saber. Observe a tabela do Barcelona, encontre o valor de 2 e veja probabilidade. Faça o mesmo com o Villarreal. Você quer encontrar Barcelona 2-0. Então 2 gols do Barcelona têm probabilidade de 0,2516, você multiplica 0,2516 por 0,5945, que é a probabilidade do Villarreal de marcar 0 gols. O resultado é de 0,1495762 e essa é a chance de acontecer 2-0.
Para encontrar o valor em percentual, basta dividir 1 pelo resultado para obter a porcentagem: (1 / 0,1495762) = 6.68.
Agora que temos o cálculo de Poisson mostrando a porcentagem para 2-0, é só ir nas casas de apostas ver qual a odd que eles estão nos oferecendo para Barcelona 2-0.
Se a casa está dizendo que a porcentagem de acontecer um 2-0 é maior do que a sua calculada, então você tem, segundo seus cálculos, algo de valor.
Em 2021 fiz mais de 11.700 dólares no meu grupo VIP. Clique aqui para saber mais.
E como converter odds das casas de apostas em porcentagem?
É simples, divida 1 pela odd, depois multiplique por 100 o resultado. Por exemplo na odd 8.0.
(1 / 8,0) = 0,12
(0,12 x 100) = 12%
A odd representa 12% convertendo para porcentagem.
E o exemplo se segue para qualquer outro
Agora que você sabe como calcular Poisson, precisa aprender a calcular a expectativa de gols das equipes.
Como Calcular a Expectativa de Gols?
Essa é uma parte importantíssima. Calcular a expectativa de gols é útil para o sucesso e isso requer duas variáveis para ser comparadas: “força ofensiva” e “força defensiva”.
(Neste exemplo vou utilizar apenas números concretos de gols marcados e de gols sofridos. Mas há sites que fazem o balanço desses números através da quantidade de chances criadas, de como essas chances foram criadas. Vale a pena você se familiarizar com isso)
Voltando. Para encontrar a força ofensiva, você precisa saber os resultados do número médio de gols marcados por cada equipe que queria calcular, tanto em jogos como mandante e como visitante.
Pegue também o número total de gols marcados pelos mandantes e o número total de gols marcados pelos visitantes.
Vou usar como exemplo números da temporada 2017/18 do Campeonato Espanhol:
- 567 gols foram marcados pelos mandantes nos 380 jogos: (567 / 380) = 1.492 gols por jogo
- 459 gols foram marcados pelos visitantes em 380 partidas: (459 / 380) = 1.207 gols por jogo
É preciso saber a média de gols marcados como mandante e visitante de toda a liga, porque isso ajudará na avaliação da força ofensiva de cada time.
Depois de saber isso é necessário descobrir a força defensiva, que é essencialmente o inverso dos números acima. Então, o número médio de gols concedido pelos mandantes é de 1.207, enquanto os visitantes concedem 1.492 gols. Agora você precisa calcular a média de gols marcados pela equipe que deseja calcular.
Agora um exemplo. O time A marcou 35 gols em casa na última temporada em 19 jogos, isso equivale a 1,842 gols em média por jogo. A média total dos mandantes foi de 1.492, que lhe dá uma força ofensiva de 1.235. O cálculo foi:
Dividir 35 por 19 = 1.842
Dividir 567 por 380 = 1.492
Dividindo 1.842 por 1.492 = 1.235 (a força ofensiva)
Agora precisamos calcular a força defensiva do time B. O número de gols sofridos fora de casa pelo time B foi de 25 em 19 partidas, que dá 1.315. Então se divide esse número pela média total de gols sofridos pelos visitantes, 1.492. O resultado é uma força defensiva de 0.881.
Com esses números em mãos é possível calcular a quantidade de gols que o time A provavelmente marcará contra o B, multiplicando sua força ofensiva pela força defensiva do time B. Ficando assim:
1,235 x 0,881 x 1,492 = 1,623.
E para calcular os gols do time B?
Se usa a mesma fórmula. Multiplica a média da força ofensiva do time B pela força de defesa do time A, multiplique também a média de gols marcados pelos visitantes fora de casa.
Time A sofreu 14 gols em 19 jogos = 0,736
Time B marcou 20 gols em 19 jogos = 1,052
1,052 (força ofensiva time B) x 0,736 (força defensiva time A) x 1,207 = 0,934.
Na equação de Poisson o símbolo µ será substituído pela força ofensiva.
Aprendeu a calcular de forma arcaica expectativa de gols? Então basta utilizar o resultado da expectativa de gols para substituir o símbolo µ na equação de Poisson.
Abaixo há uma caixa de diálogos. Pergunte qualquer coisa.